Étude d’une fonction Linéaire
Comprendre l’Étude d’une fonction Linéaire
Soit la fonction linéaire \(f\) définie par
\[ f(x) = 3x – 5 \]
Questions :
1. Représentation graphique
- Tracez la représentation graphique de la fonction \(f\) dans un repère orthogonal.
2. Calculs d’images
- Calculez \(f(0)\), \(f(2)\) et \(f(-1)\).
3. Calcul d’antécédents
- Déterminez un antécédent de \(4\) par \(f\).
- Existe-t-il plusieurs antécédents de \(4\) ? Justifiez votre réponse.
4. Interprétation géométrique
- Quel est le coefficient directeur de la droite représentant la fonction \(f\) ? Quelle est son interprétation géométrique ?
- Déterminez l’ordonnée à l’origine de cette droite.
5. Résolution d’équation
- Résolvez l’équation \(f(x) = 0\).
6. Comparaison de fonctions
- Considérons une seconde fonction linéaire \(g\) définie par \(g(x) = -\frac{1}{2}x + 3\). Sans tracer la représentation graphique de \(g\), comparez les pentes de \(f\) et \(g\). Quelle conclusion pouvez-vous tirer sur les directions des droites représentant \(f\) et \(g\) dans le même repère ?
Correction : Étude d’une fonction Linéaire
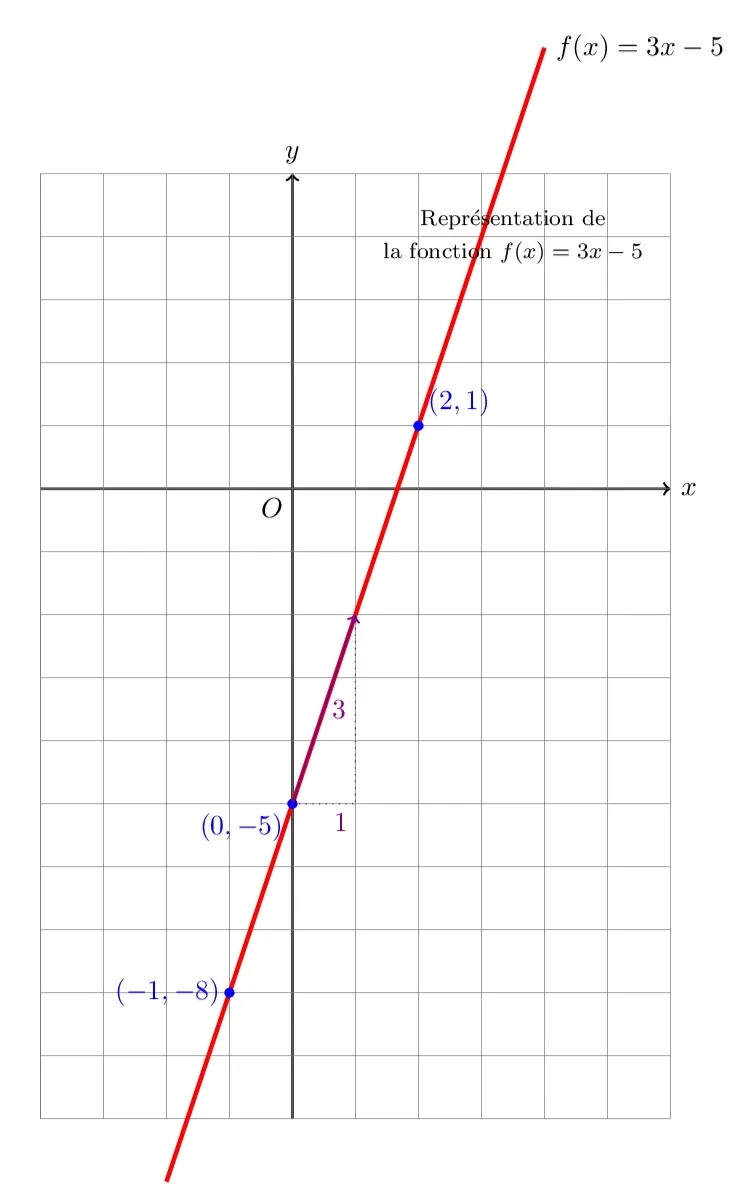
1. Représentation graphique
Pour tracer la représentation graphique de \( f(x)=3x-5 \) dans un repère orthogonal, il est utile de connaître quelques points caractéristiques de la droite. L’ordonnée à l’origine est donnée par \( f(0) \) (voir question 4). On peut calculer des images pour choisir des points (voir question 2).
Ainsi, en représentant sur un repère, on place le point \( (0, f(0)) \) et on trace une droite qui monte de 3 unités verticalement pour chaque unité horizontale (car le coefficient directeur est 3).
2. Calculs d’images
Calculons les images de quelques valeurs :
- Pour \( x = 0 \) :
\[f(0) = 3 \times 0 – 5 = -5.\] - Pour \( x = 2 \) :
\[f(2) = 3 \times 2 – 5 = 6 – 5 = 1.\] - Pour \( x = -1 \) :
\[f(-1) = 3 \times (-1) – 5 = -3 – 5 = -8.\]
Les points obtenus sont donc ;
- \( (0,-5) \)
- \( (2,1) \)
- \( (-1,-8) \).
3. Calcul d’antécédents
Pour trouver un antécédent de 4 par \( f \), on cherche \( x \) tel que :
\[f(x) = 4.\]
On écrit l’équation :
\[3x – 5 = 4.\]
Pour résoudre cette équation :
- Ajoutons d’abord 5 des deux côtés :
\[3x = 9.\] - Puis divisons par 3 :
\[x = 3.\]
Ainsi, l’antécédent de 4 par \( f \) est \( x = 3 \).
Justification sur l’unicité : La fonction \( f \) est une fonction linéaire (de la forme \( ax+b \) avec \( a \neq 0 \)). Elle est donc bijective, ce qui implique qu’elle associe à chaque image un unique antécédent. Il n’existe donc qu’un seul antécédent de 4.
4. Interprétation géométrique
- Coefficient directeur :
Dans l’expression \( f(x)=3x-5 \), le coefficient directeur est \( 3 \).
- Interprétation géométrique :
Cela signifie que pour chaque unité d’augmentation sur l’axe des abscisses, l’image augmente de 3 unités. La droite est donc assez pentue et croît rapidement.
- Ordonnée à l’origine :
L’ordonnée à l’origine est la valeur de \( f(x) \) lorsque \( x = 0 \). Nous avons déjà trouvé que :
\[f(0) = -5.\]
Cela signifie que la droite coupe l’axe des ordonnées au point \( (0,-5) \).
5. Résolution d’équation
Pour résoudre l’équation \( f(x) = 0 \), on pose :
\[3x – 5 = 0.\]
En isolant \( x \) :
- Ajouter 5 :
\[3x = 5.\] - Diviser par 3 :
\[x = \frac{5}{3}.\]
Ainsi, la solution de l’équation \( f(x) = 0 \) est \( x = \frac{5}{3} \).
6. Comparaison de fonctions
Considérons la fonction \( g \) définie par
\[g(x) = -12x + 3.\]
- Pour \( f(x)=3x-5 \), le coefficient directeur est \( 3 \).
- Pour \( g(x)=-12x+3 \), le coefficient directeur est \( -12 \).
Comparaison des pentes : La pente de \( f \) est positive (3) ce qui signifie que la droite est croissante. La pente de \( g \) est négative (-12) ce qui signifie que la droite est décroissante.
Conclusion sur les directions : Les droites représentant \( f \) et \( g \) ont des directions opposées : la droite de \( f \) monte vers la droite, tandis que la droite de \( g \) descend vers la droite.
Étude d’une fonction Linéaire

0 commentaires