Étude de la fonction f
Comprendre l’Étude de la fonction f
Soit la fonction \(f\) définie sur \(\mathbb{R}\) par :
\[ f(x) = \frac{x^2 – 4}{x – 2} \]
Questions :
1. Simplifiez l’expression de \(f(x)\) autant que possible. (Indice : effectuez une factorisation du numérateur.)
2. Déterminez le domaine de définition de \(f\). (Rappelez-vous que le dénominateur d’une fraction ne peut pas être nul.)
3. Calculez \(f(0)\), \(f(1)\), et \(f(3)\). Ces calculs permettent d’illustrer comment obtenir l’image de certains éléments du domaine par la fonction \(f\).
4. Déterminez si la fonction \(f\) est continue sur son domaine de définition. Expliquez votre raisonnement.
5. Représentez graphiquement la fonction \(f\) sur l’intervalle \([-2, 5]\). Identifiez clairement le point, s’il existe, où la fonction n’est pas définie.
6. Conclusion: À partir de la forme simplifiée de \(f(x)\) et de votre graphique, quelles observations pouvez-vous faire sur le comportement de la fonction \(f\) près de la valeur pour laquelle elle n’est pas définie ?
Correction : Étude de la fonction f
1. Simplification de l’expression de \( f(x) \)
La fonction est donnée par :
\[f(x)=x^2-4x-2.\]
Pour simplifier \(f(x)\), on cherche à factoriser le polynôme. On calcule d’abord le discriminant :
\[\Delta=(-4)^2-4\times1\times(-2)\]
\[\Delta=16+8=24.\]
Comme \(\Delta=24\) n’est pas un carré parfait, la factorisation se fait avec des racines irrationnelles. Les solutions de l’équation \(x^2-4x-2=0\) sont :
\[x = \frac{4 \pm \sqrt{24}}{2}\]
\[x = \frac{4 \pm 2\sqrt{6}}{2}\]
\[x=2\pm\sqrt{6}.\]
On peut alors écrire :
\[f(x)=(x-(2+\sqrt{6}))(x-(2-\sqrt{6})).\]
Cette forme factorisée est la forme simplifiée de \(f(x)\).
2. Domaine de définition de \(f\)
La fonction \(f(x)\) est un polynôme (ou, après factorisation, le produit de deux expressions polynomiales). Or, un polynôme est défini pour tout \(x\in\mathbb{R}\).
Donc, le domaine de définition est :
\[D(f)=\mathbb{R}.\]
Remarque : la mention « dénominateur » dans l’énoncé rappelle que, dans une fraction, le dénominateur ne doit pas être nul. Ici, il n’y a pas de fraction, ce qui confirme que \(f\) est définie pour tout réel.
3. Calcul de \(f(0)\), \(f(1)\) et \(f(3)\)
Pour \(x=0\) :
\[f(0)=0^2-4\times0-2\]
\[f(0)=-2.\]
Pour \(x=1\) :
\[f(1)=1^2-4\times1-2\]
\[f(1)=1-4-2\]
\[f(1)=-5.\]
Pour \(x=3\) :
\[f(3)=3^2-4\times3-2\]
\[f(3)=9-12-2\]
\[f(3)=-5.\]
4. Continuité de la fonction \(f\)
Les fonctions polynomiales sont continues sur \(\mathbb{R}\).
Ainsi, \(f\) est continue sur son domaine de définition, c’est-à-dire sur \(\mathbb{R}\).
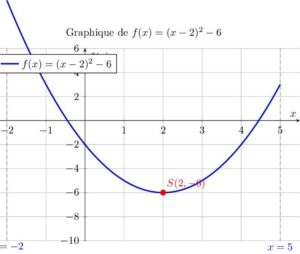
5. Représentation graphique de \(f\) sur l’intervalle \([-2,5]\)
Pour tracer le graphique de \(f\), on peut également écrire \(f(x)\) sous forme canonique en complétant le carré :
\[f(x)=x^2-4x-2\]
\[f(x)=(x^2-4x+4)-4-2\]
\[f(x)=(x-2)^2-6.\]
La forme canonique nous indique que la parabole a pour sommet le point \(S(2,-6)\) et s’ouvre vers le haut (le coefficient de \((x-2)^2\) est positif).
Sur l’intervalle \([-2,5]\), la fonction est définie en tout point et le graphique est une courbe lisse continue.
Point à noter : Il n’existe aucun point sur \([-2,5]\) (ni ailleurs) où la fonction serait non définie, car \(f\) est un polynôme.
6. Conclusion
Puisque \(f(x)\) est un polynôme, elle est définie et continue pour tout \(x\in\mathbb{R}\).
Il n’existe donc aucun point (ni sur \([-2,5]\), ni ailleurs) où la fonction ne soit pas définie.
Dès lors, il n’y a pas de comportement singulier ou d’asymptote à étudier.
Les observations principales sont donc :
- La forme factorisée \((x-(2+\sqrt{6}))(x-(2-\sqrt{6}))\) montre que la fonction a deux racines réelles.
- La forme canonique \((x-2)^2-6\) révèle que le minimum de \(f\) est atteint en \(x=2\) et vaut \(-6\).
- La fonction est définie et continue partout, sans point de discontinuité.
Résumé des résultats
- Forme simplifiée :
\[f(x)=(x-(2+\sqrt{6}))(x-(2-\sqrt{6})).\]
- Domaine de définition :
\[D(f)=\mathbb{R}.\] - Calculs d’images :
\[f(0)=-2,\quad f(1)=-5,\quad f(3)=-5.\] - Continuité : \(f\) est continue sur \(\mathbb{R}\).
- Graphique sur \([-2,5]\) : La parabole de \(f\), de sommet \(S(2,-6)\), est tracée sur \([-2,5]\) sans interruption, car \(f\) est définie partout.
- Aucune valeur n’étant exclue du domaine, la fonction \(f\) présente un comportement régulier sur \(\mathbb{R}\), et notamment près de toutes les valeurs de \(x\).
Étude de la fonction f

0 commentaires