Vecteurs et Produit Scalaire dans le Plan
Comprendre les Vecteurs et Produit Scalaire dans le Plan
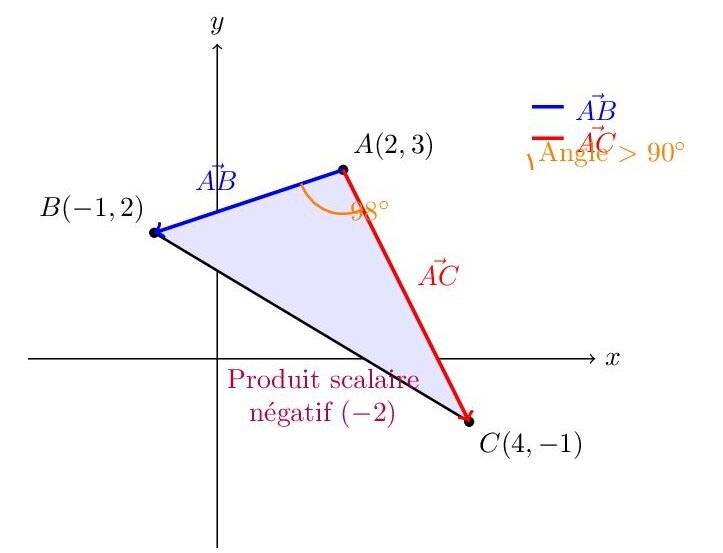
Dans un repère orthonormé \((O; \vec{i}, \vec{j})\), on considère les points \(A(2,3)\), \(B(-1,2)\), et \(C(4,-1)\).
Questions:
1. Vecteurs et coordonnées :
- Calculer les coordonnées des vecteurs \(\vec{AB}\) et \(\vec{AC}\).
2. Produit scalaire :
Calculer le produit scalaire \(\vec{AB} \cdot \vec{AC}\) de deux manières :
- Par les coordonnées.
- En utilisant la définition géométrique du produit scalaire \(\vec{u} \cdot \vec{v} = \|\vec{u}\| \cdot \|\vec{v}\| \cdot \cos(\theta)\), où \(\theta\) est l’angle entre \(\vec{u}\) et \(\vec{v}\).
3. Angle entre deux vecteurs :
- Déduire l’angle \(\theta\) entre \(\vec{AB}\) et \(\vec{AC}\).
4. Application géométrique :
- Utiliser le résultat du produit scalaire pour déterminer si le triangle \(ABC\) est acutangle, obtusangle ou rectangle.
Correction : Vecteurs et Produit Scalaire dans le Plan
1. Vecteurs et coordonnées :
Coordonnées du vecteur \(\vec{AB}\) :
On utilise la formule :
\[\vec{AB} = B – A.\]
Puis on calcule des coordonnées :
- Abscisse : \(-1 – 2 = -3\)
- Ordonnée :\(2 – 3 = -1\)
Ainsi,
\[\vec{AB} = (-3,\ -1).\]
Coordonnées du vecteur \(\vec{AC}\) :
On utilise la formule :
\[\vec{AC} = C – A.\]
Puis on calcule des coordonnées :
- Abscisse : \(4 – 2 = 2\).
- Ordonnée : \(-1 – 3 = -4\).
Ainsi,
\[\vec{AC} = (2,\ -4).\]
2. Produit scalaire :
On va calculer le produit scalaire de \(\vec{AB}\) et \(\vec{AC}\) de deux manières.
a) Par les coordonnées :
Rappel de la formule :
\[\vec{AB} \cdot \vec{AC} = x_1 \cdot x_2 + y_1 \cdot y_2.\]
Pour \(\vec{AB} = (-3,\ -1)\) et \(\vec{AC} = (2,\ -4)\) :
- Produit des abscisses : (\(-3) \times 2 = -6\).
- Produit des ordonnées : (\(-1) \times (-4) = 4\).
La somme des deux produits donne :
\[-6 + 4 = -2.\]
Ainsi,
\[\vec{AB} \cdot \vec{AC} = -2.\]
b) En utilisant la définition géométrique :
La formule géométrique du produit scalaire est :
\[\vec{AB} \cdot \vec{AC} = \|\vec{AB}\| \cdot \|\vec{AC}\| \cdot \cos \theta,\]
où \(\theta\) est l’angle entre les vecteurs.
- Calcul de \(\vec{AB}\) :
\[\|\vec{AB}\| = \sqrt{(-3)^2 + (-1)^2}\]
\[|\vec{AB}\| = \sqrt{9+1} = \sqrt{10}.\]
- Calcul de \(\vec{AC}\) :
\[\|\vec{AC}\| = \sqrt{(2)^2 + (-4)^2} = \sqrt{4+16}\]
\[\|\vec{AC}\| = \sqrt{20} = 2\sqrt{5}.\]
On connaît déjà \(\vec{AB} \cdot \vec{AC} = -2\) (de la méthode par coordonnées).
- On écrit alors :
\[-2 = \sqrt{10} \times (2\sqrt{5}) \times \cos \theta.\] - Calcul du produit des normes :
\[\sqrt{10} \times (2\sqrt{5}) = 2\sqrt{50}.\] - Or, \(\sqrt{50} = 5\sqrt{2}\), donc :
\[2\sqrt{50} = 10\sqrt{2}.\] - L’équation devient donc :
\[-2 = 10\sqrt{2} \cdot \cos \theta,\]
ce qui donne :
\[\cos \theta = \frac{-2}{10\sqrt{2}} = \frac{-1}{5\sqrt{2}}.\]
3. Angle entre deux vecteurs :
Pour trouver l’angle \(\theta\) entre \(\vec{AB}\) et \(\vec{AC}\), on utilise la formule obtenue :
\[\cos \theta = \frac{-1}{5\sqrt{2}}.\]
L’angle \(\theta\) est donc :
\[\theta = \arccos\left(\frac{-1}{5\sqrt{2}}\right).\]
Pour une valeur approchée, on calcule numériquement :
\[5\sqrt{2} \approx 5 \times 1.414 \approx 7.07,\]
donc
\[\cos \theta \approx \frac{-1}{7.07}\]
\[\cos \theta\approx -0.1414,\]
Ainsi avec l’arccosinus :
\[\theta \approx \arccos(-0.1414)\]
\[\theta \approx 98^\circ.\]
4. Application géométrique
Pour déterminer la nature du triangle ABC, on s’appuie sur le signe du produit scalaire (ou de l’angle) entre les vecteurs associés aux côtés :
Ici, le produit scalaire \(\vec{AB} \cdot \vec{AC}\) est négatif (-2), ce qui implique que l’angle entre \(\vec{AB}\) et \(\vec{AC}\) est supérieur à \(90^\circ\) (puisque \(\cos \theta < 0\). En particulier, l’angle en A, formé par les vecteurs \(\vec{AB}\) et \(\vec{AC}\), est d’environ \(98^\circ\), c’est-à-dire obtus.
Ainsi, le triangle ABC possède un angle obtus et est donc obtusangle.
Résumé des résultats :
- Vecteurs :
\(\vec{AB} = (-3, -1)\)
\(\vec{AC} = (2, -4)\).
- Produit scalaire :
Par coordonnées : \(\vec{AB} \cdot \vec{AC} = -2\)
Par définition géométrique : \(\cos \theta = \frac{-1}{5\sqrt{2}}\)
- L’angle est calculé comme :
\(\arccos\left(\frac{-1}{5\sqrt{2}}\right)\), ce qui montre que \(\theta\) est obtus car \(\cos \theta < 0\).
- Nature du triangle ABC :
Le triangle ABC est obtusangle (il possède un angle obtus en A).
Vecteurs et Produit Scalaire dans le Plan
0 commentaires